Tables: Exercise-5
Overview:
| Questions and Answers Type: | MCQ (Multiple Choice Questions). |
| Main Topic: | Data Interpretation. |
| Data Interpretation Sub-topic: | Tables Questions and Answers. |
| Number of Questions: | 5 Questions with Solutions. |
Directions: In the following table, the number of employees working in five companies and the respective ratio of male and female employees have been given. Study the following table carefully and answer the questions given below it.
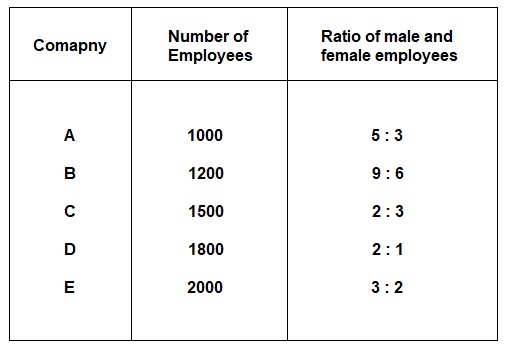
- What is the respective ratio between the number of males in the comapany D and number of males in the company C?
- 1:2
- 2:1
- 2:3
- 3:2
Answer: (b) 2:1Solution: Number of males in the company D, $$ = \frac{2}{3} \times 1800 $$ $$ = 1200 $$ Number of males in the company C, $$ = \frac{2}{5} \times 1500 $$ $$ = 600 $$ Hence, Required ratio $$ = 1200 : 600 $$ $$ = 2 : 1 $$
- The number of female employees working in the company B is what percent of total employees working in that company?
- 10%
- 20%
- 30%
- 40%
Answer: (d) 40%Solution: Required percentage, $$ = \frac{6}{15} \times 100 $$ $$ = 40 \ \% $$
- What is the average number of employees in all companies together?
- 800
- 1000
- 1200
- 1500
Answer: (d) 1500Solution: Average number of employees in all companies together, $$ = \frac{7500}{5} = 1500 $$
- What is the number of female employees in company A and B together?
- 855
- 842
- 822
- 810
Answer: (a) 855Solution: Number of female employees in company A, $$ = \frac{3}{8} \times 1000 $$ $$ = 375 $$ Number of female employees in company B, $$ = \frac{6}{15} \times 1200 $$ $$ = 480 $$ Hence, total number of female employees in company A and B together, $$ = 375 + 480 = 855 $$
- What is the number of male employees in company E?
- 1500
- 1200
- 1000
- 500
Answer: (b) 1200Solution: Number of male employees in company E, $$ = \frac{3}{5} \times 2000 $$ $$ = 1200 $$