Tables: Exercise-2
Overview:
| Questions and Answers Type: | MCQ (Multiple Choice Questions). |
| Main Topic: | Data Interpretation. |
| Data Interpretation Sub-topic: | Tables Questions and Answers. |
| Number of Questions: | 5 Questions with Solutions. |
Directions: Study the following table carefully and answer the questions given below it.
A number of students from a college X who appeared and qualified in a competitive exam during the last five years.
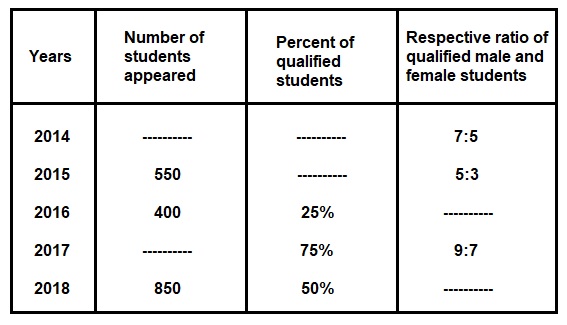
- In 2014, 3000 students appeared at the exam and 50% of them qualified. In 2018, the ratio between qualified male and female students was 2:3. What is the total number of female students who qualified in these two years?
- 980
- 960
- 945
- 935
Answer: (a) 980Solution: Number of students who qualified in 2014, $$ = \frac{3000 \times 50}{100} $$ $$ = 1500 $$ Number of female students in 2014 who qualified, $$ = \frac{5}{12} \times 1500 = 625 $$ Number of students who qualified in 2018, $$ = \frac{850 \times 50}{100} = 425 $$ Number of female students who qualified in 2018, $$ = \frac{3}{5} \times 425 = 255 $$ Hence, total number of female students who qualified in these two years, $$ = 625 + 255 = 980 $$
- In 2017, what percent of female students did qualify in the exam among all qualified students?
- 35.23%
- 38.25%
- 43.75%
- 45.50%
Answer: (c) 43.75%Solution: Percent of female qualified students in 2017, $$ = \frac{7}{16} \times 100 $$ $$ = 43.75 \ \% $$
- In 2015, If 60% of appeared students did qualify, then find how many male students did qualify in the exam?
- 215
- 212
- 208
- 206
Answer: (d) 206Solution: Number of qualified students in 2015, $$ = \frac{550 \times 60}{100} $$ $$ = 330 $$ Number of qualified male students in 2015, $$ = \frac{5}{8} \times 330 $$ $$ = 206.25 \approx 206 $$
- In 2016, a total of 80 male students did qualify. What is the respective ratio between males and females who had qualified in 2016?
- 2:3
- 4:1
- 3:5
- 4:5
Answer: (b) 4:1Solution: Number of qualified students in 2016, $$ = \frac{400 \times 25}{100} = 100 $$ Number of female students who qualified in 2016, $$ = 100 - 80 = 20 $$ Hence, the ratio between males and females who qualified in 2016, $$ = 80 : 20 $$ $$ = 4 : 1 $$
- Find the total number of disqualified students in the years 2016 and 2018 together?
- 680
- 710
- 725
- 755
Answer: (c) 725Solution: Number of disqualified students in the year 2016, $$ = \frac{400 \times (100 - 25)}{100} $$ $$ = \frac{400 \times 75}{100} $$ $$ = 300 $$ Number of disqualified students in the year 2018, $$ = \frac{850 \times (100 - 50)}{100} $$ $$ = \frac{850 \times 50}{100} $$ $$ = 425 $$ Hence, total number of disqualified students in the years 2016 and 2018 together, $$ = 300 + 425 $$ $$ = 725 $$