Line Graph: Exercise-8
Overview:
| Questions and Answers Type: | MCQ (Multiple Choice Questions). |
| Main Topic: | Data Interpretation. |
| Data Interpretation Sub-topic: | Line Graph Questions and Answers. |
| Number of Questions: | 5 Questions with Solutions. |
Directions: Study the following graph carefully and answer the questions given below it.
Percent profit earned by two companies A and B by selling the refrigerator over the years.
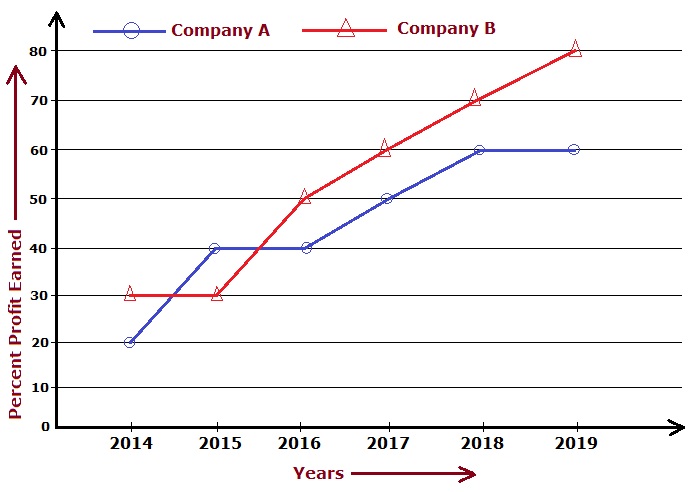
- If the profit earned by company A in the year 2017 was $10,000 then what was the total income of company A in the same year?
- $30,000
- $32,000
- $35,000
- $38,000
Answer: (a) $30,000Solution: \(Percentage \ Profit =\) \(\left[\frac{Profit \ earned}{Total \ investment} \times 100\right]\)\(Total \ investment =\) \(\left[\frac{10,000}{50} \times 100\right]\)\( = $20,000\)Hence total income $$ = 10,000 + 20,000 $$ $$ = $30,000 $$
- If the amount invested by the two companies in the year 2015 were equal then what was the ratio of the total profit of company A to that of B in the year 2015?
- 1 : 2
- 2 : 3
- 4 : 3
- 5 : 3
Answer: (c) 4 : 3Solution: Let the amount invested by the two companies in the year 2015 = \(x\) dollarsThe profit earned by the company A in the year 2015. $$ = \frac{40}{100} \times x $$ $$ = \frac{2x}{5} \ dollars $$ The profit earned by the company B in the year 2015. $$ = \frac{30}{100} \times x $$ $$ = \frac{3x}{10} \ dollars $$ Required ratio $$ = \frac{\frac{2x}{5}}{\frac{3x}{10}} $$ $$ = \frac{2x}{5} \times \frac{10}{3x} $$ $$ = \frac{4}{3} $$ $$ = 4 : 3 $$
- If the amount invested by company B in the year 2016 was $12,500 and the income of 2016 is equal to the investment in 2017 then how much profit earned by the company B in the year 2017?
- $11,250
- $11,320
- $11,370
- $11,410
Answer: (a) $11,250Solution: The amount invested by company B in 2016.$$ = $12,500 $$ The profit earned by company B in 2016.\(Percentage \ Profit =\) \(\left[\frac{Profit \ earned}{Total \ investment} \times 100\right]\)\(50 = \left[\frac{Profit \ earned}{12,500} \times 100\right]\)\(Profit \ earned = $6,250\)The total income of company B in 2016.$$ = 12,500 + 6,250 $$ $$ = $18,750 $$ Hence the profit earned by the company B in the year 2017. $$ = \left[\frac{60}{100} \times 18,750\right] $$ $$ = $11,250 $$
- If the income of company A in 2017 and 2018 were equal, and the amount invested in 2017 was $12,200 then what was the amount invested in 2018?
- $11,221.5
- $11,437.5
- $11,532.5
- $11,642.5
Answer: (b) $11,437.5Solution: The amount invested by company A in 2017 = \($12,200\)Total income of company A in 2017 = \(12,200 + Profit \ earned\)\(= 12,200 + \frac{50}{100} \times 12,200\)\(= 12,200 + 6,100\)\(= $18,300\)The amount invested by company A in 2018.$$ = \left[\frac{100}{160} \times 18,300\right] $$ $$ = $11,437.5 $$
- If the investment of company B in 2018 and 2019 were equal then what was the difference between the profits earned in two years if the income in 2019 was $18,200?
- $1011
- $1020
- $1022
- $1024
Answer: (a) $1011Solution: The investment of company B in 2019.$$ = \left[\frac{100}{180} \times 18,200\right] $$ $$ = $10,111.12 $$ $$ \approx $10,111 $$ The profit of company B in 2019.$$ = 18,200 - 10,111 $$ $$ = $8,089 $$ The profit of company B in 2018.$$ = \left[\frac{70}{100} \times 10,111\right] $$ $$ = $7,077.7 $$ $$ \approx $7,078 $$ Required difference $$ = 8,089 - 7,078 $$ $$ = $1,011 $$