Line Graph: Exercise-2
Overview:
| Questions and Answers Type: | MCQ (Multiple Choice Questions). |
| Main Topic: | Data Interpretation. |
| Data Interpretation Sub-topic: | Line Graph Questions and Answers. |
| Number of Questions: | 5 Questions with Solutions. |
Directions: Study the following graph carefully and answer the questions given below it.
Number of tourists visiting a country from city A and city B during six different months.
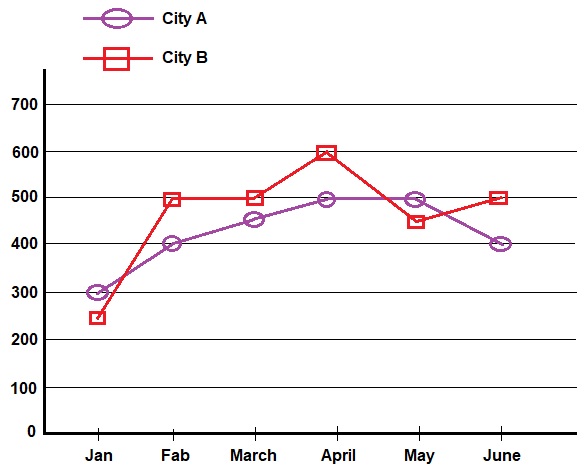
- What is the difference between average number of tourists from city A and city B during all the months together?
- 30
- 38
- 40
- 42
Answer: (d) 42Solution: Average number of tourists in city A, $$ = \frac{300 + 400 + 450 + 500 + 500 + 400}{6} $$ $$ = \frac{2550}{6} = 425 $$ average number of tourists in city B, $$ = \frac{250 + 500 + 500 + 600 + 450 + 500}{6} $$ $$ = \frac{2800}{6} $$ $$ = 466.67 \approx 467 $$ Hence, the required difference, $$ = 467 - 425 = 42 $$
- What is the respective ratio between the total number of tourists from city A and B during January, Fabruary and March taken together?
- 24:25
- 23:24
- 23:25
- 24:22
Answer: (c) 23:25Solution: Tourists from city A during January, Fabruary and March taken together, $$ = 300 + 400 + 450 $$ $$ = 1150 $$ Tourists from city B during January, Fabruary and March taken together, $$ = 250 + 500 + 500 $$ $$ = 1250 $$ Hence, required ratio, $$ = 1150 : 1250 $$ $$ = 23 : 25 $$
- By what percent is the number of tourists from city A less than that from city B in the month of April?
- 10%
- 20%
- 30%
- 40%
Answer: (b) 20%Solution: Required percent, $$ = \frac{600 - 500}{500} \times 100 $$ $$ = 20 \ \% $$
- By what percent the number of tourists from city B increased in April than that from the month January?
- 140%
- 120%
- 100%
- 75%
Answer: (a) 140%Solution: Required percent, $$ = \frac{600 - 250}{250} \times 100 $$ $$ = 140 \ \% $$
- By what percent approximately is the total number of tourists from city A less than that of all the tourists from city B taking all the months together?
- 5%
- 7%
- 8%
- 9%
Answer: (d) 9%Solution: total tourists from city A = 2550total tourists from city B = 2800Required percent, $$ = \frac{2800 - 2550}{2800} \times 100 $$ $$ = 8.92 \ \% \approx 9 \ \% $$