Polynomial Remainder Theorem Important Formulas, Definitions, & Examples:
Overview:
| Topic Included: | Formulas, Definitions & Exmaples. |
| Main Topic: | Quantitative Aptitude. |
| Quantitative Aptitude Sub-topic: | Number System Aptitude Notes & Questions. |
| Questions for practice: | 10 Questions & Answers with Solutions. |
What is Polynomial:
A polynomial is an algebraic expression consisting of variables, coefficients, constants, and positive integer exponents, that are connected with operators such as addition, subtraction, multiplication but not by division.
Polynomial Example:
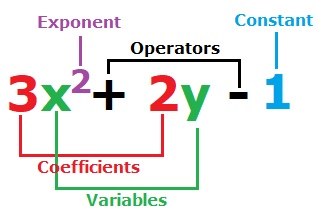
Polynomial Degree:
The highest value of the exponent of the variable decides the degree of any polynomial expression. the above equation is a 2-degree polynomial equation because the highest value of the exponent of variable \(x\) is 2.
\(2\), Here the degree is 0 because It is a constant. It is also called zero polynomial.
\(2x - 1\), Here the degree is 1 because the highest value of the exponent of the variable \(x\) is 1. It is a linear equation or linear polynomial or binomial.
\(3x^2 + 2x - 1\), Here the degree is 2 because the highest value of the exponent of the variable \(x\) is 2. It is a quadratic polynomial or trinomial.
\(4x^3 + 3x^2 + 2x - 1\), Here the degree is 3 because the highest value of the exponent of the variable \(x\) is 3. It is a cubic polynomial.
What is Polynomial Remainder Theorem:
Polynomial Remainder Theorem is used to find the remainder of any polynomial algebraic expression. According to Polynomial remainder theorem-
$$ (k + x)^n = k^n + n C_1 k^{n-1} x^1 + n C_2 k^{n-2} x^2 +.............n C_{n-1} k^1 x^{n-1} + x^n$$
$$ (k + x)^n =$$ $$= k^n + n C_1 k^{n-1} x^1 + n C_2 k^{n-2} x^2 +...\\..........n C_{n-1} k^1 x^{n-1} + x^n$$
Dividing by k into both sides, we will get.
$$ \frac{(k + x)^n}{k} = \frac{k^n + n C_1 k^{n-1} x^1 + n C_2 k^{n-2} x^2 +.............n C_{n-1} k^1 x^{n-1} + x^n}{k}$$
$$ \frac{(k + x)^n}{k} =$$ $$ = \frac{k^n + n C_1 k^{n-1} x^1 + n C_2 k^{n-2} x^2 +...\\..........n C_{n-1} k^1 x^{n-1} + x^n}{k}$$
In the above polynomial remainder theorem equation, the last term \(x^n\) is the only term that is not divisible by \(k\), but the rest of the terms contains \('k'\) which is completely divisible by \(k\), that's why the Remainder of parent equation will be. $$ \frac{(k + x)^n}{k} = \frac{x^n}{k} $$
Polynomial Remainder Theorem Examples:
Example(1): Find the remainder of the expression \(\frac{7^{99}}{6}\) by using the polynomial remainder theorem?
Solution: According to the polynomial remainder theorem, $$\frac{7^{99}}{6} = \frac{(6 + 1)^{99}}{6}$$ $$ = \frac{1^{99}}{6} = 1 \ (Remainder) $$
Example(2): Find the remainder of the expression \(\frac{2x^2 - 3x - 1}{x - 3}\) by using the polynomial remainder theorem?
Solution: According to the polynomial remainder theorem, $$ \require{enclose} \begin{array}{r} 2x + 3 \\[-3pt] x - 3 \enclose{longdiv}{2x^2 - 3x - 1} \\[-3pt] \underline{2x^2 - 6x}\phantom{ - 1} \\[-3pt] 3x - 1 \\[-3pt] \underline{3x - 9} \\[-3pt] 0 + 8 \end{array} $$ Here 8 is the remainder and \((2x + 3)\) is the quotient.
Example(3): Find the remainder of the expression \(\frac{8^{100}}{6}\) by using the polynomial remainder theorem?
Solution: According to the polynomial remainder theorem, $$\frac{8^{100}}{6} = \frac{(6 + 2)^{100}}{6} = \frac{2^{100}}{6}$$ $$= \frac{2^{99} \times 2}{6} = \frac{(2^3)^{33} \times 2}{6}$$ $$= \frac{(6 + 2)^{3} \times 2}{6} = \frac{2^3 \times 2}{6}$$ $$= \frac{8 \times 2}{6} = \frac{(6 + 2) \times 2}{6}$$ $$= \frac{2 \times 2}{6} = \frac{4}{6} = 4 \ (Remainder)$$
Example(4): Find the remainder of the expression \(\frac{2^{100}}{7}\) by using the polynomial remainder theorem?
Solution: According to the polynomial remainder theorem, $$\frac{2^{100}}{7} = \frac{(2)^{99} \times 2}{7} = \frac{(2^3)^{33} \times 2}{7}$$ $$= \frac{(7 + 1)^{33} \times 2}{7} = \frac{1^{33} \times 2}{7}$$ $$= \frac{1 \times 2}{7} = 2 \ (Remainder)$$
Example(5): Find the remainder of the expression \(\frac{2^{10}}{3}\) by using the polynomial remainder theorem?
Solution: According to the polynomial remainder theorem, $$\frac{2^{10}}{3} = \frac{2^9 \times 2}{3} = \frac{(2^3)^3 \times 2}{3}$$ $$= \frac{(3 + 5)^3 \times 2}{3} = \frac{5^3 \times 2}{3}$$ $$= \frac{(3 + 2)^{3} \times 2}{3} = \frac{2^3 \times 2}{3}$$ $$= \frac{16}{3} = 1 \ (Remainder)$$