Direction and Distance: Exercise-5
- A boy starts from home in the early morning and walks straight for 8 km facing the sun. Then, he takes a right turn and walks for 3 km. Then, he turns right again and walks for 2 km, and then he turns left and walks for 1 km. Again he turns right and walks 1 km. Then, he turns right and travels for 4 km straight. How is he from the starting point?
- 3 km
- 4 km
- 5 km
- 6 km
Answer: (c) 5 kmSolution: 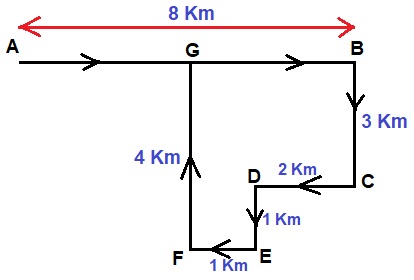 Here, $$ BG = CD + EF $$ $$ BG = 3 \ km $$ Hence,$$ AG = AB - BG $$ $$ AG = 8 - 3 $$ $$ = 5 \ km $$
Here, $$ BG = CD + EF $$ $$ BG = 3 \ km $$ Hence,$$ AG = AB - BG $$ $$ AG = 8 - 3 $$ $$ = 5 \ km $$
 Here, $$ BG = CD + EF $$ $$ BG = 3 \ km $$ Hence,$$ AG = AB - BG $$ $$ AG = 8 - 3 $$ $$ = 5 \ km $$
Here, $$ BG = CD + EF $$ $$ BG = 3 \ km $$ Hence,$$ AG = AB - BG $$ $$ AG = 8 - 3 $$ $$ = 5 \ km $$- Rohit drives a car from Bengaluru to Mysore. After 80 km he turns right and goes 50 km. After that, he again turns to his right and moves on 70 km. Finally, he turns to his right and stops after moving a distance of 50 km. At what distance is Rohit now from Bengaluru?
- 5 km
- 10 km
- 15 km
- 20 km
Answer: (b) 10 kmSolution: 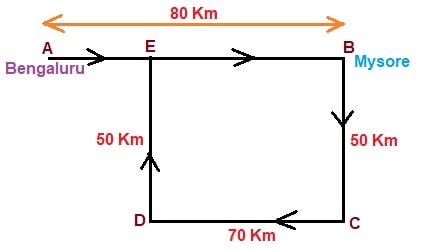 Here,$$ BE = CD = 70 \ km $$ Hence,$$ AE = AB - BE $$ $$ AE = 80 - 70 $$ $$ AE = 10 \ km $$
Here,$$ BE = CD = 70 \ km $$ Hence,$$ AE = AB - BE $$ $$ AE = 80 - 70 $$ $$ AE = 10 \ km $$
 Here,$$ BE = CD = 70 \ km $$ Hence,$$ AE = AB - BE $$ $$ AE = 80 - 70 $$ $$ AE = 10 \ km $$
Here,$$ BE = CD = 70 \ km $$ Hence,$$ AE = AB - BE $$ $$ AE = 80 - 70 $$ $$ AE = 10 \ km $$- Ram cycled 10 km Southward from his home, turned right and cycled 6 km, turned right and cycled 10 km, turned left and cycled 15 km. How many kilometers will he have cycled straight to reach home?
- 21 km
- 24 km
- 25 km
- 27 km
Answer: (a) 21 kmSolution: 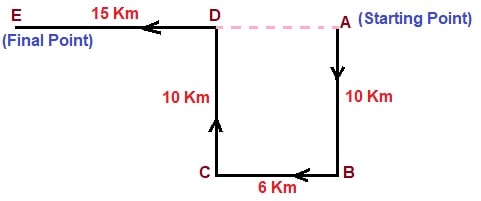 Here,$$ AD = BC = 6 km $$ Hence,$$ AE = AD + DE $$ $$ AE = 6 + 15 $$ $$ = 21 \ km $$
Here,$$ AD = BC = 6 km $$ Hence,$$ AE = AD + DE $$ $$ AE = 6 + 15 $$ $$ = 21 \ km $$
 Here,$$ AD = BC = 6 km $$ Hence,$$ AE = AD + DE $$ $$ AE = 6 + 15 $$ $$ = 21 \ km $$
Here,$$ AD = BC = 6 km $$ Hence,$$ AE = AD + DE $$ $$ AE = 6 + 15 $$ $$ = 21 \ km $$- A boy travelled 20 km to the East, he turned left and went 12 km, he again turned left and went 20 km. How far is he now from the starting point?
- 10 km
- 12 km
- 15 km
- 18 km
Answer: (b) 12 kmSolution: 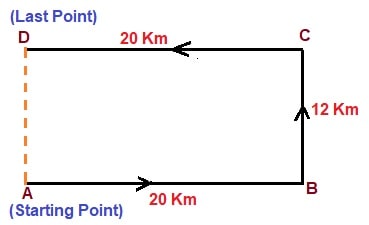 Here,$$ AB = CD = 20 \ km $$ similarly,$$ BC = AD = 12 \ km $$ Hence, the boy is 12 km far from his starting point.
Here,$$ AB = CD = 20 \ km $$ similarly,$$ BC = AD = 12 \ km $$ Hence, the boy is 12 km far from his starting point.
 Here,$$ AB = CD = 20 \ km $$ similarly,$$ BC = AD = 12 \ km $$ Hence, the boy is 12 km far from his starting point.
Here,$$ AB = CD = 20 \ km $$ similarly,$$ BC = AD = 12 \ km $$ Hence, the boy is 12 km far from his starting point.- A girl left home and cycled 15 km Southward, turned right and cycled 7.5 km and again turned right and cycled 15 km and then turned left and cycled 15 km. How many kilometers will she now have to cycle in the straight line to reach her home?
- 22.5 km
- 25.5 km
- 27.5 km
- 27.5 km
Answer: (a) 22.5 kmSolution: 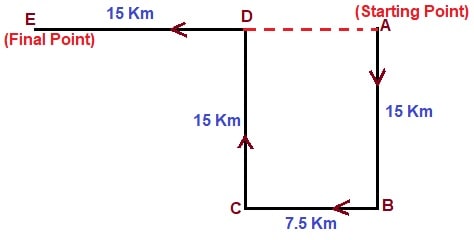 Here,$$ AB = CD = 15 \ km $$ Similarly,$$ BC = AD = 7.5 \ km $$ And, $$ DE = 15 \ km $$ Hence, the girl will have to cycle from E to A, to reach her home.$$ EA = DE + AD $$ $$ EA = 15 + 7.5 $$ $$ = 22.5 \ km $$
Here,$$ AB = CD = 15 \ km $$ Similarly,$$ BC = AD = 7.5 \ km $$ And, $$ DE = 15 \ km $$ Hence, the girl will have to cycle from E to A, to reach her home.$$ EA = DE + AD $$ $$ EA = 15 + 7.5 $$ $$ = 22.5 \ km $$
 Here,$$ AB = CD = 15 \ km $$ Similarly,$$ BC = AD = 7.5 \ km $$ And, $$ DE = 15 \ km $$ Hence, the girl will have to cycle from E to A, to reach her home.$$ EA = DE + AD $$ $$ EA = 15 + 7.5 $$ $$ = 22.5 \ km $$
Here,$$ AB = CD = 15 \ km $$ Similarly,$$ BC = AD = 7.5 \ km $$ And, $$ DE = 15 \ km $$ Hence, the girl will have to cycle from E to A, to reach her home.$$ EA = DE + AD $$ $$ EA = 15 + 7.5 $$ $$ = 22.5 \ km $$- Mr.Bruce walked 30 km towards South and then he turned to his left and moved 25 km. He again turned to his left and walked 30 km. Thereafter, he turned to his right and walked 20 km. What is the distance and direction of his present location with reference to the starting point?
- 25 km
- 35 km
- 45 km
- 55 km
Answer: (c) 45 kmSolution: 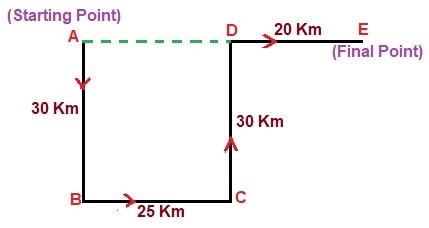 Here,$$ AB = CD = 30 \ km $$ Similarly,$$ BC = AD = 25 \ km $$ Hence, the distance of his present location with reference to the starting point,$$ AE = AD + DE $$ $$ = 25 + 20 $$ $$ = 45 \ km $$ And he is to the East from his starting point.
Here,$$ AB = CD = 30 \ km $$ Similarly,$$ BC = AD = 25 \ km $$ Hence, the distance of his present location with reference to the starting point,$$ AE = AD + DE $$ $$ = 25 + 20 $$ $$ = 45 \ km $$ And he is to the East from his starting point.
 Here,$$ AB = CD = 30 \ km $$ Similarly,$$ BC = AD = 25 \ km $$ Hence, the distance of his present location with reference to the starting point,$$ AE = AD + DE $$ $$ = 25 + 20 $$ $$ = 45 \ km $$ And he is to the East from his starting point.
Here,$$ AB = CD = 30 \ km $$ Similarly,$$ BC = AD = 25 \ km $$ Hence, the distance of his present location with reference to the starting point,$$ AE = AD + DE $$ $$ = 25 + 20 $$ $$ = 45 \ km $$ And he is to the East from his starting point.- Ram walks Southward and covers 20 km distance. He then turns to his right and walks 30 km, after which he turns to his right again and walks 20 km. What is the Shortest distance from his start to end point?
- 10 km
- 20 km
- 30 km
- 40 km
Answer: (c) 30 kmSolution: 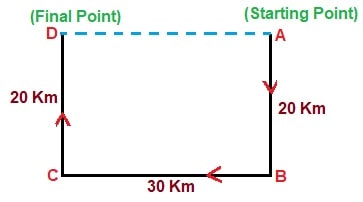 Here,$$ AB = CD = 20 \ km $$ Similarly,$$ BC = AD = 30 \ km $$ Hence, the shortest distance from endpoint to the starting point will be from A to D.$$ AD = 30 \ km $$
Here,$$ AB = CD = 20 \ km $$ Similarly,$$ BC = AD = 30 \ km $$ Hence, the shortest distance from endpoint to the starting point will be from A to D.$$ AD = 30 \ km $$
 Here,$$ AB = CD = 20 \ km $$ Similarly,$$ BC = AD = 30 \ km $$ Hence, the shortest distance from endpoint to the starting point will be from A to D.$$ AD = 30 \ km $$
Here,$$ AB = CD = 20 \ km $$ Similarly,$$ BC = AD = 30 \ km $$ Hence, the shortest distance from endpoint to the starting point will be from A to D.$$ AD = 30 \ km $$- A car driver starts driving from the home, drives 4 km towards North, takes a left turn and drives for 10 km. He then takes a left turn and drives for 20 km before taking a left turn again and driving for further 10 km. The driver finally takes a left turn and drives 2 km, before stopping. How far and towards which direction should the driver drive to reach the home again?
- 14 km, towards North
- 14 km, towards South
- 16 km, towards East
- 16 km, towards South
Answer: (a) 14 km, towards NorthSolution: 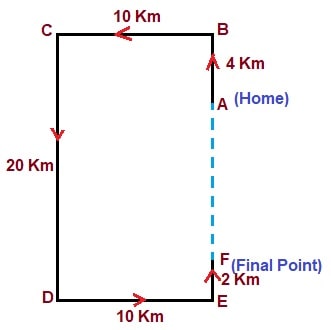 Here,$$ BC = DE = 10 \ km $$ Similarly,$$ CD = BE = 20 \ km $$ And,$$ AB = 4 \ km $$ $$ EF = 2 \ km $$ Now,$$ AF = BE - (AB + EF) $$ $$ AF = 20 - (4 + 2) $$ $$ = 14 \ km $$ Hence, It is clear that the driver needs to drive 14 km towards North direction from the endpoint F.
Here,$$ BC = DE = 10 \ km $$ Similarly,$$ CD = BE = 20 \ km $$ And,$$ AB = 4 \ km $$ $$ EF = 2 \ km $$ Now,$$ AF = BE - (AB + EF) $$ $$ AF = 20 - (4 + 2) $$ $$ = 14 \ km $$ Hence, It is clear that the driver needs to drive 14 km towards North direction from the endpoint F.
 Here,$$ BC = DE = 10 \ km $$ Similarly,$$ CD = BE = 20 \ km $$ And,$$ AB = 4 \ km $$ $$ EF = 2 \ km $$ Now,$$ AF = BE - (AB + EF) $$ $$ AF = 20 - (4 + 2) $$ $$ = 14 \ km $$ Hence, It is clear that the driver needs to drive 14 km towards North direction from the endpoint F.
Here,$$ BC = DE = 10 \ km $$ Similarly,$$ CD = BE = 20 \ km $$ And,$$ AB = 4 \ km $$ $$ EF = 2 \ km $$ Now,$$ AF = BE - (AB + EF) $$ $$ AF = 20 - (4 + 2) $$ $$ = 14 \ km $$ Hence, It is clear that the driver needs to drive 14 km towards North direction from the endpoint F.- A boy goes 2 km South and then takes a turn towards the West and moves 8 km. He then again turns towards the North and goes 10 km, before turning towards East and moving up to 8 km. How far is he now from the starting point?
- 5 km
- 6 km
- 7 km
- 8 km
Answer: (d) 8 kmSolution: 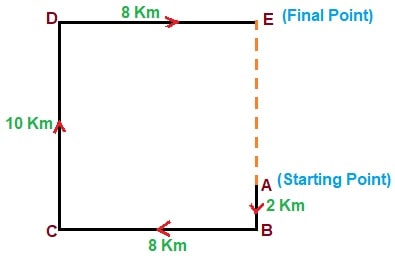 Here,$$ BC = DE = 8 \ km $$ Similarly,$$ CD = BE = 10 \ km $$ And,$$ AB = 2 \ km $$ Now, we need to find out the distance between the A and E points.$$ AE = BE - AB $$ $$ = 10 - 2 $$ $$ = 8 \ km $$ Hence, the boy is 8 km far from his starting point.
Here,$$ BC = DE = 8 \ km $$ Similarly,$$ CD = BE = 10 \ km $$ And,$$ AB = 2 \ km $$ Now, we need to find out the distance between the A and E points.$$ AE = BE - AB $$ $$ = 10 - 2 $$ $$ = 8 \ km $$ Hence, the boy is 8 km far from his starting point.
 Here,$$ BC = DE = 8 \ km $$ Similarly,$$ CD = BE = 10 \ km $$ And,$$ AB = 2 \ km $$ Now, we need to find out the distance between the A and E points.$$ AE = BE - AB $$ $$ = 10 - 2 $$ $$ = 8 \ km $$ Hence, the boy is 8 km far from his starting point.
Here,$$ BC = DE = 8 \ km $$ Similarly,$$ CD = BE = 10 \ km $$ And,$$ AB = 2 \ km $$ Now, we need to find out the distance between the A and E points.$$ AE = BE - AB $$ $$ = 10 - 2 $$ $$ = 8 \ km $$ Hence, the boy is 8 km far from his starting point.- Two people P and Q start moving from the same point towards opposite directions. Both, P and Q travel 4 km. Then, P turns towards the right and travels 3 km. And Q also turns towards and travels 3 km. What is the shortest distance between P and Q?
- 10 km
- 12 km
- 15 km
- 18 km
Answer: (a) 10 kmSolution: 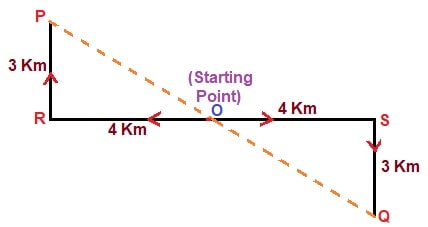 Here,$$ RO = OS = 4 \ km $$ Similarly,$$ PR = QS = 3 \ km $$ And,$$ PO = OQ $$ Now,$$ PO = \sqrt{(PR)^2 + (RO)^2} $$ $$ = \sqrt{3^2 + 4^2} $$ $$ = \sqrt{9 + 16} $$ $$ = \sqrt{25} = 5 $$ So,$$ PO = OQ = 5 \ km $$ Hence, the shortest distance between P and Q,$$ PQ = PO + OQ $$ $$ = 5 + 5 $$ $$ = 10 \ km $$
Here,$$ RO = OS = 4 \ km $$ Similarly,$$ PR = QS = 3 \ km $$ And,$$ PO = OQ $$ Now,$$ PO = \sqrt{(PR)^2 + (RO)^2} $$ $$ = \sqrt{3^2 + 4^2} $$ $$ = \sqrt{9 + 16} $$ $$ = \sqrt{25} = 5 $$ So,$$ PO = OQ = 5 \ km $$ Hence, the shortest distance between P and Q,$$ PQ = PO + OQ $$ $$ = 5 + 5 $$ $$ = 10 \ km $$
 Here,$$ RO = OS = 4 \ km $$ Similarly,$$ PR = QS = 3 \ km $$ And,$$ PO = OQ $$ Now,$$ PO = \sqrt{(PR)^2 + (RO)^2} $$ $$ = \sqrt{3^2 + 4^2} $$ $$ = \sqrt{9 + 16} $$ $$ = \sqrt{25} = 5 $$ So,$$ PO = OQ = 5 \ km $$ Hence, the shortest distance between P and Q,$$ PQ = PO + OQ $$ $$ = 5 + 5 $$ $$ = 10 \ km $$
Here,$$ RO = OS = 4 \ km $$ Similarly,$$ PR = QS = 3 \ km $$ And,$$ PO = OQ $$ Now,$$ PO = \sqrt{(PR)^2 + (RO)^2} $$ $$ = \sqrt{3^2 + 4^2} $$ $$ = \sqrt{9 + 16} $$ $$ = \sqrt{25} = 5 $$ So,$$ PO = OQ = 5 \ km $$ Hence, the shortest distance between P and Q,$$ PQ = PO + OQ $$ $$ = 5 + 5 $$ $$ = 10 \ km $$