Direction and Distance: Exercise-4
- The time in a clock is quarter past twelve. If the hour hand points to the East, find which is the direction opposite to the minute hand?
- North
- South
- East
- West
Answer: (a) NorthSolution: 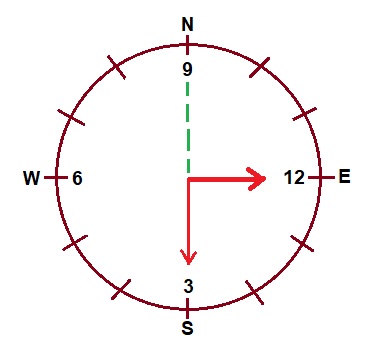 North is the direction opposite to the minute hand.
North is the direction opposite to the minute hand.
 North is the direction opposite to the minute hand.
North is the direction opposite to the minute hand.- A man is facing West. He turns \(45^{o}\) in the anti-clockwise direction and then \(180^{o}\) in the clockwise direction and then \(270^{o}\) in the anti-clockwise direction. Which direction is he facing now?
- North
- South-East
- East
- North-West
Answer: (b) South-EastSolution: Now he is facing South-East direction.
- A girl is facing West. She turns \(45^{o}\) in the clockwise direction and then \(180^{o}\) in the same direction and then \(270^{o}\) in the anti-clockwise direction. Which direction is she facing now?
- North-East
- South
- South-West
- West
Answer: (c) South-WestSolution: now, she is facing South-West direction.
- If South-East becomes North and North-East becomes West and all the rest directions are changed in the same manner. What will be the direction for the West?
- North-East
- North-West
- South-East
- South-West
Answer: (c) South-EastSolution: Original Directions: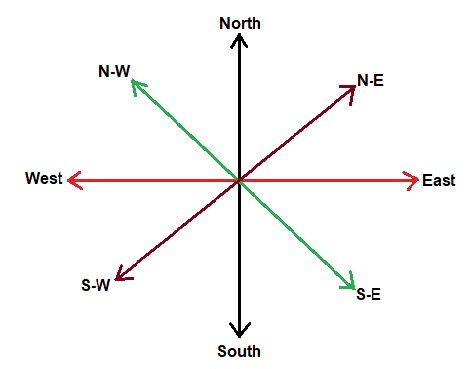 New Directions:
New Directions: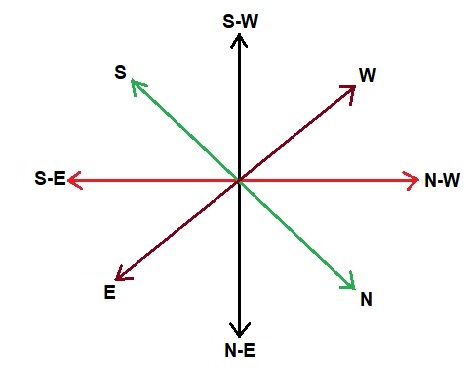 The new direction for the West is South-East.
The new direction for the West is South-East.
 New Directions:
New Directions: The new direction for the West is South-East.
The new direction for the West is South-East.- A girl walks 3 km. from point A to B. She turns right at \(90^{o}\) and walks 5 km. up to point C. She, then again turns right at \(90^{o}\) and walks 10 km. up to point D. She, then again takes right turn at \(90^{o}\) and walks 5 km. up to point E. She, then again takes right turn at \(90^{o}\) and walks 2 km. and reaches point F. Find the distance between point A and point F?
- 5 Km.
- 10 Km.
- 15 Km.
- 20 Km.
Answer: (a) 5 Km.Solution: 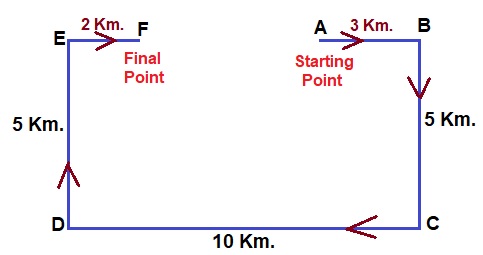 Here $$ CD = BE = 10 \ Km. $$ Hence, distance between points A and F.$$ = CD - (EF + AB) $$ $$ = BE - (EF + AB) $$ $$ = 10 - (2 + 3) $$ $$ = 5 \ Km. $$
Here $$ CD = BE = 10 \ Km. $$ Hence, distance between points A and F.$$ = CD - (EF + AB) $$ $$ = BE - (EF + AB) $$ $$ = 10 - (2 + 3) $$ $$ = 5 \ Km. $$
 Here $$ CD = BE = 10 \ Km. $$ Hence, distance between points A and F.$$ = CD - (EF + AB) $$ $$ = BE - (EF + AB) $$ $$ = 10 - (2 + 3) $$ $$ = 5 \ Km. $$
Here $$ CD = BE = 10 \ Km. $$ Hence, distance between points A and F.$$ = CD - (EF + AB) $$ $$ = BE - (EF + AB) $$ $$ = 10 - (2 + 3) $$ $$ = 5 \ Km. $$- A girl travels 2 km. due North then travels 3 km. due East and further travels 2 km. due North. How far he is from the starting point?
- 5 Km.
- 10 Km.
- 15 Km.
- 20 Km.
Answer: (a) 5 Km.Solution: 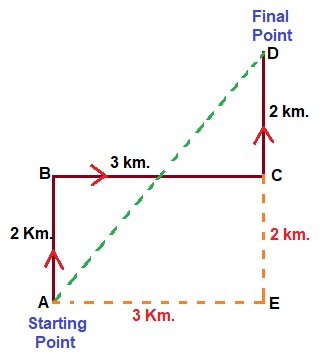 Where, $$ CD = CE = 2 \ Km. $$ $$ BC = AE = 3 \ Km. $$ Now, according to the Pythagoras theorem. $$ AD^2 = AE^2 + DE^2 $$ $$ AD^2 = 3^2 + 4^2 $$ $$ AD = \sqrt{9 + 16} $$ $$ AD = \sqrt{25} = 5 \ km. $$
Where, $$ CD = CE = 2 \ Km. $$ $$ BC = AE = 3 \ Km. $$ Now, according to the Pythagoras theorem. $$ AD^2 = AE^2 + DE^2 $$ $$ AD^2 = 3^2 + 4^2 $$ $$ AD = \sqrt{9 + 16} $$ $$ AD = \sqrt{25} = 5 \ km. $$
 Where, $$ CD = CE = 2 \ Km. $$ $$ BC = AE = 3 \ Km. $$ Now, according to the Pythagoras theorem. $$ AD^2 = AE^2 + DE^2 $$ $$ AD^2 = 3^2 + 4^2 $$ $$ AD = \sqrt{9 + 16} $$ $$ AD = \sqrt{25} = 5 \ km. $$
Where, $$ CD = CE = 2 \ Km. $$ $$ BC = AE = 3 \ Km. $$ Now, according to the Pythagoras theorem. $$ AD^2 = AE^2 + DE^2 $$ $$ AD^2 = 3^2 + 4^2 $$ $$ AD = \sqrt{9 + 16} $$ $$ AD = \sqrt{25} = 5 \ km. $$- A man starts from his home and walks 20 km. towards the South. Then, he turns right and walks 10 km, again he turns right and goes 20 km. Finally, he turns right and walks 6 km. At what distance is he from his home?
- 1 Km.
- 2 Km.
- 3 Km.
- 4 Km.
Answer: (d) 4 Km.Solution: 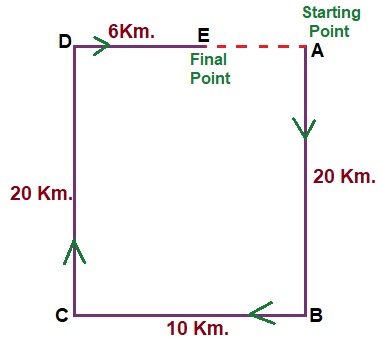 $$ BC = AD = 10 \ Km. $$ Hence, $$ AE = AD - DE $$ $$ AE = 10 - 6 = 4 \ Km. $$
$$ BC = AD = 10 \ Km. $$ Hence, $$ AE = AD - DE $$ $$ AE = 10 - 6 = 4 \ Km. $$
 $$ BC = AD = 10 \ Km. $$ Hence, $$ AE = AD - DE $$ $$ AE = 10 - 6 = 4 \ Km. $$
$$ BC = AD = 10 \ Km. $$ Hence, $$ AE = AD - DE $$ $$ AE = 10 - 6 = 4 \ Km. $$- A girl travels 8 km. West and then turns left and travels 3 km. and further turns left and travels 15 km. How far is she now from the starting point?
- \(\sqrt{29} \ Km.\)
- \(\sqrt{58} \ Km.\)
- \(\sqrt{63} \ Km.\)
- \(\sqrt{76} \ Km.\)
Answer: (b) \(\sqrt{58} \ Km.\)Solution: 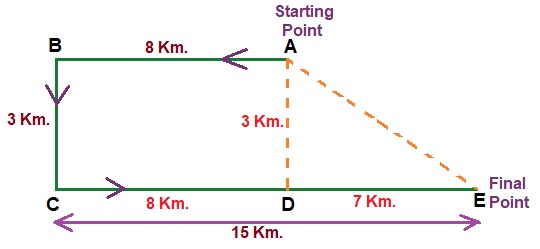 $$ BC = AD = 3 \ Km. $$ $$ AB = CD = 8 \ Km. $$ Hence, $$ DE = CE - CD $$ $$ DE = 15 - 8 = 7 \ Km. $$ By Pythagoras theorem $$ AE^2 = AD^2 + DE^2 $$ $$ AE^2 = 3^2 + 7^2 $$ $$ AE = \sqrt{9 + 49} $$ $$ AE = \sqrt{58} \ Km. $$
$$ BC = AD = 3 \ Km. $$ $$ AB = CD = 8 \ Km. $$ Hence, $$ DE = CE - CD $$ $$ DE = 15 - 8 = 7 \ Km. $$ By Pythagoras theorem $$ AE^2 = AD^2 + DE^2 $$ $$ AE^2 = 3^2 + 7^2 $$ $$ AE = \sqrt{9 + 49} $$ $$ AE = \sqrt{58} \ Km. $$
 $$ BC = AD = 3 \ Km. $$ $$ AB = CD = 8 \ Km. $$ Hence, $$ DE = CE - CD $$ $$ DE = 15 - 8 = 7 \ Km. $$ By Pythagoras theorem $$ AE^2 = AD^2 + DE^2 $$ $$ AE^2 = 3^2 + 7^2 $$ $$ AE = \sqrt{9 + 49} $$ $$ AE = \sqrt{58} \ Km. $$
$$ BC = AD = 3 \ Km. $$ $$ AB = CD = 8 \ Km. $$ Hence, $$ DE = CE - CD $$ $$ DE = 15 - 8 = 7 \ Km. $$ By Pythagoras theorem $$ AE^2 = AD^2 + DE^2 $$ $$ AE^2 = 3^2 + 7^2 $$ $$ AE = \sqrt{9 + 49} $$ $$ AE = \sqrt{58} \ Km. $$- A woman started to move in the direction of the South. After moving 5 Km she turned to her right and goes 5 km, again she turned right and goes 5 Km. Now how far is she and in which direction from her starting point?
- 5 Km, North
- 5 Km, South
- 5 Km, East
- 5 Km, West
Answer: (d) 5 Km, WestSolution: 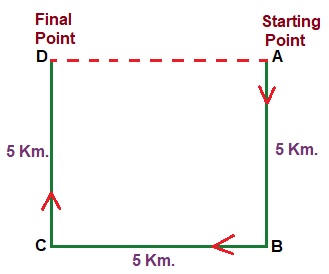 $$ AD = BC = 5 \ Km. $$ She is 5 km. far from her starting point and in the West direction from her starting point.
$$ AD = BC = 5 \ Km. $$ She is 5 km. far from her starting point and in the West direction from her starting point.
 $$ AD = BC = 5 \ Km. $$ She is 5 km. far from her starting point and in the West direction from her starting point.
$$ AD = BC = 5 \ Km. $$ She is 5 km. far from her starting point and in the West direction from her starting point.- A boy moves 20 Km North, then he turns right and moves 25 Km. Again, he turns right and moves 15 Km. Finally, he turns right and reaches 25 Km. How far is he from his starting point?
- 2 Km.
- 5 km.
- 10 Km.
- 15 Km.
Answer: (b) 5 Km.Solution: 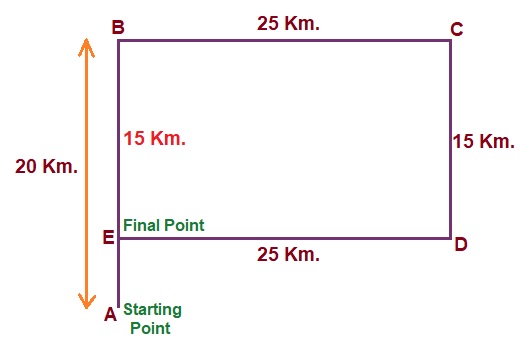 $$ BE = CD = 15 \ Km. $$ Then, $$ AE = AB - BE $$ $$ AE = 20 - 15 $$ $$ AE = 5 \ Km. $$
$$ BE = CD = 15 \ Km. $$ Then, $$ AE = AB - BE $$ $$ AE = 20 - 15 $$ $$ AE = 5 \ Km. $$
 $$ BE = CD = 15 \ Km. $$ Then, $$ AE = AB - BE $$ $$ AE = 20 - 15 $$ $$ AE = 5 \ Km. $$
$$ BE = CD = 15 \ Km. $$ Then, $$ AE = AB - BE $$ $$ AE = 20 - 15 $$ $$ AE = 5 \ Km. $$