Pie Chart: Exercise-7
Overview:
| Questions and Answers Type: | MCQ (Multiple Choice Questions). |
| Main Topic: | Data Interpretation. |
| Data Interpretation Sub-topic: | Pie Graph Questions and Answers. |
| Number of Questions: | 5 Questions with Solutions. |
Directions: Study the following pie chart carefully and answer the questions given below it.
Distribution of areas (in acres) for growing various fruits.
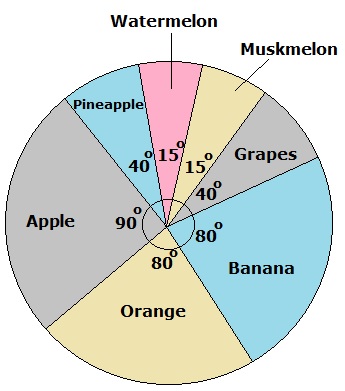
- If the total area goes up by 10%, and the area under grapes production goes up by 25%, then what will be the angle for grapes in the new pie chart?
- \(40.25^0\)
- \(43.05^0\)
- \(45.45^0\)
- \(42.15^0\)
Answer: (c) \(45.45^0\)Solution: If the total area is \(x\) then.New total area $$ = \frac{110 \ x}{100} $$ $$ = \frac{11 \ x}{10} $$ The current area under grapes $$ = \frac{40 \ x}{360} $$ $$ = \frac{x}{9} $$ The new area under grapes $$ = \left[\frac{125}{100} \times \frac{x}{9}\right] $$ $$ = \frac{5x}{36} $$ New angle for grapes in the new pie chart.$$ \left[\frac{\frac{5x}{36}}{\frac{11x}{10}} \times 360\right] $$ $$ = \left[\frac{5x}{36} \times \frac{10}{11x} \times 360\right] $$ $$ = 45.45^0 $$
- If the area under banana was five thousand acres then what was the area under pineapple (in thousand acres)?
- 1.5 Thousand acres
- 2.5 Thousand acres
- 3.0 Thousand acres
- 3.5 Thousand acres
Answer: (b) 2.5 Thousand acresSolution: Let the total area is \(x\) thousand acres.Area under banana $$ = \frac{80}{360} \times x $$ $$ = \frac{2x}{9} $$ Area under pineapple $$ = \frac{40}{360} \times x $$ $$ = \frac{x}{9} $$ If \(\frac{2x}{9} = 5\) thousand acres then \(x = 22.5\) thousand acres.Hence area under pineapple.$$ = \frac{22.5}{9} $$ $$ = 2.5 \ thousand \ acres $$
- If the yield per acre of orange was 20% more than that of grapes, then the production of grapes is approximately what percent of that of orange?
- 42 %
- 40 %
- 34 %
- 32 %
Answer: (a) 42 %Solution: Let the total area = \(x\)then area under the orange $$ = \frac{80x}{360} $$ $$ = \frac{2x}{9} $$ Area under grapes $$ = \frac{40x}{360} $$ $$ = \frac{x}{9} $$ Let yield of grapes per acre = \(y\) tons.Then the yield of grapes per acre. $$ = \frac{120y}{100} $$ $$ = \frac{6y}{5} \ tons $$ Required percentage $$ = \left[\frac{\frac{x}{9} \times y}{\frac{2x}{9} \times \frac{6y}{5}} \times 100\right] \ \% $$ $$ = \left[\frac{xy}{9} \times \frac{45}{12xy} \times 100\right] $$ $$ = 41.67 \ \% $$ $$ \approx 42 \ \% $$
- If the production of apple is three times that of pineapple, then what is the ratio between the yield per acre of apple and pineapple?
- 2 : 3
- 3 : 2
- 3 : 4
- 4 : 3
Answer: (d) 4 : 3Solution: Let the total area = \(x\)Then the area under the apple. $$ = \frac{90x}{360} $$ $$ = \frac{x}{4} $$ Area under pineapple $$ = \frac{40x}{360} $$ $$ = \frac{x}{9} $$ Let the production of the pineapple be \(P\) tons.Then the production of apple \(= 3P\) tons.The yield of apple per acre $$ = \frac{3P}{\frac{x}{4}} $$ $$ = \frac{12P}{x} $$ The yield of pineapple per acre $$ = \frac{P}{\frac{x}{9}} $$ $$ = \frac{9P}{x} $$ Required ratio $$ = \left[\frac{\frac{12P}{x}}{\frac{9P}{x}}\right] $$ $$ = \frac{12}{9} $$ $$ = \frac{4}{3} $$ $$ = 4 : 3 $$
- Which one fruit production area contributes to 25% of the total area under all fruits production?
- Apple
- Orange
- Banana
- Pineapple
Answer: (a) AppleSolution: For 25% of the total area, the angle should be \(90^0\) and apple is the only fruit with \(90^0\) angle on the pie chart. Hence the apple production area contributes to 25% of the total area.