Pie Chart: Exercise-4
Overview:
| Questions and Answers Type: | MCQ (Multiple Choice Questions). |
| Main Topic: | Data Interpretation. |
| Data Interpretation Sub-topic: | Pie Graph Questions and Answers. |
| Number of Questions: | 5 Questions with Solutions. |
Directions: Study the following pie-chart carefully to answer the questions given below.
Total number of passengers in six different planes are 1800.
Percentage of passengers in six different planes A, B, C, D, E and F in pie-chart given below.
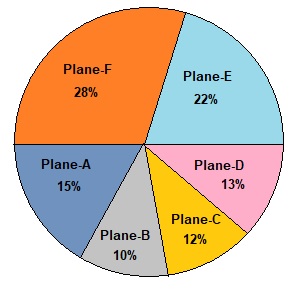
- What is the average number of passengers travelling in Plane-B, Plane-E and Plane-F together?
- 280
- 300
- 340
- 360
Answer: (d) 360Solution: Total percentsge of passengers in all three planes are 60%, then average number of passengers in Plane-A, Plane-B and Plane-C together, $$ = \frac{1800 \times 60}{100 \times 3} $$ $$ = 360 \ Passengers $$
- If cost of one ticket is Rs.1200, then find the total amount paid by the passengers of Plane-A?
- 280,000
- 312,000
- 324,000
- 332,000
Answer: (c) 324,000Solution: Number of passengers in Plane-A, $$ = \frac{1800 \times 15}{100} $$ $$ = 270 $$ The total amount paid by the passengers of Plane-A, $$ = 270 \times 1200 $$ $$ = 324,000 \ Rs. $$
- Number of passengers in Plane-A is approximately what percentage of the total number of passengers in Plane-C and Plane-D together?
- 40%
- 50%
- 60%
- 70%
Answer: (c) 60%Solution: Required Percentage, $$ = \frac{15}{25} \times 100 $$ $$ = 60 \ \% $$
- What is the difference between the number of passengers in Plane-F and Plane-E?
- 122
- 108
- 100
- 96
Answer: (b) 108Solution: Difference between the number of passengers in Plane-F and Plane-E, $$ = \frac{1800 \times 6}{100} $$ $$ = 108 \ Passengers $$
- Find the total number of passengers in Plane-B, Plane-C and Plane-D together?
- 630
- 660
- 690
- 710
Answer: (a) 630Solution: Number of passengers in all three planes, $$ = \frac{1800 \times 35}{100} $$ $$ = 630 \ Passengers $$