Bar Diagrams: Exercise-7
Overview:
| Questions and Answers Type: | MCQ (Multiple Choice Questions). |
| Main Topic: | Data Interpretation. |
| Data Interpretation Sub-topic: | Bar Graph Questions and Answers. |
| Number of Questions: | 5 Questions with Solutions. |
Directions: Study the following bar diagram carefully and answer the questions given below it.
The total number of students from different schools appeared and qualified for a competitive exam.
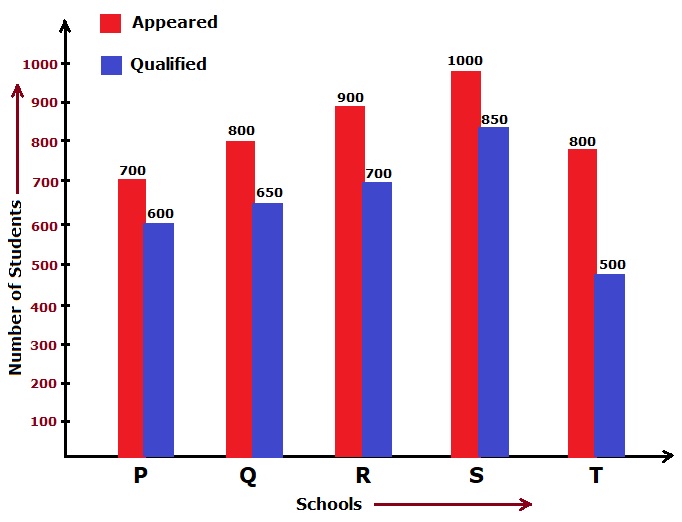
- Find the average number of students qualified in the examination from schools P and Q is what percentage of the average number of students appeared for the examination from the same schools?
- 83.34 %
- 85.23 %
- 88.20 %
- 89.15 %
Answer: (a) 83.34 %Solution: The average number of students qualified from schools P and Q. $$ = \frac{1}{2} \ (600 + 650) $$ $$ = \frac{1}{2} \ (1250) $$ $$ = 625 $$ The Average number of students appeared from schools P and Q. $$ = \frac{1}{2} \ (700 + 800) $$ $$ = \frac{1}{2} \ (1500) $$ $$ = 750 $$ Required percentage $$ = \left[\frac{625}{750} \times 100\right] \ \% $$ $$ = 83.34 \ \% $$
- Find out the ratio of the number of students who appeared to the number of students qualified in the exam from school S?
- 15:11
- 13:9
- 20:17
- 22:19
Answer: (c) 20:17Solution: Required ratio $$ = \frac{1000}{850} $$ $$ = \frac{20}{17} $$ $$ = 20:17 $$
- Find out the ratio of the number of students who appeared in the exam from school S to the number of students who appeared in the exam from school T?
- 2:3
- 4:3
- 5:4
- 6:5
Answer: (c) 5:4Solution: Required ratio $$ = \frac{1000}{800} $$ $$ = \frac{10}{8} $$ $$ = \frac{5}{4} = 5:4 $$
- Find the number of students qualified for the exam, from the school S is approximately what percent of the total number of students qualified for the exam from all the schools together?
- 20 %
- 26 %
- 29 %
- 32 %
Answer: (b) 26 %Solution: Number of students qualified for the exam from the school S = 850Number of students qualified for the exam from all the schools together = \(600 + 650 + 700 + 850 + 500\) = \(3300\)Required percentage $$ = \left[\frac{850}{3300} \times 100\right] \ \% $$ $$ = 25.76 \ \% $$ $$ \approx 26 \ \% $$
- Find the difference between the average number of students who appeared and qualified from all the schools together in the exam?
- 210
- 200
- 180
- 175
Answer: (c) 180Solution: The average number of students appeared for the exam from all the schools together. = \(\frac{1}{5} \ (700 + 800 + 900 + 1000 + 800)\)= \(\frac{1}{5} \times 4200\)= 840The average number of students qualified for the exam from all the schools together. = \(\frac{1}{5} \ (600 + 650 + 700 + 850 + 500)\)= \(\frac{1}{5} \times 3300\)= 660Requaired difference = \(840 - 660\) = \(180s\)