Bar Diagrams: Exercise-10
Overview:
| Questions and Answers Type: | MCQ (Multiple Choice Questions). |
| Main Topic: | Data Interpretation. |
| Data Interpretation Sub-topic: | Bar Graph Questions and Answers. |
| Number of Questions: | 5 Questions with Solutions. |
Directions: Study the following bar diagram carefully and answer the questions given below it.
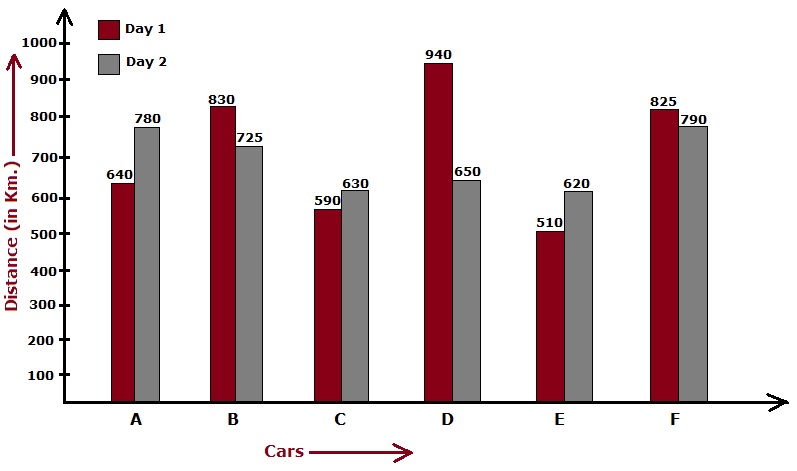
Distance covered (in Km) by six cars on two different days.
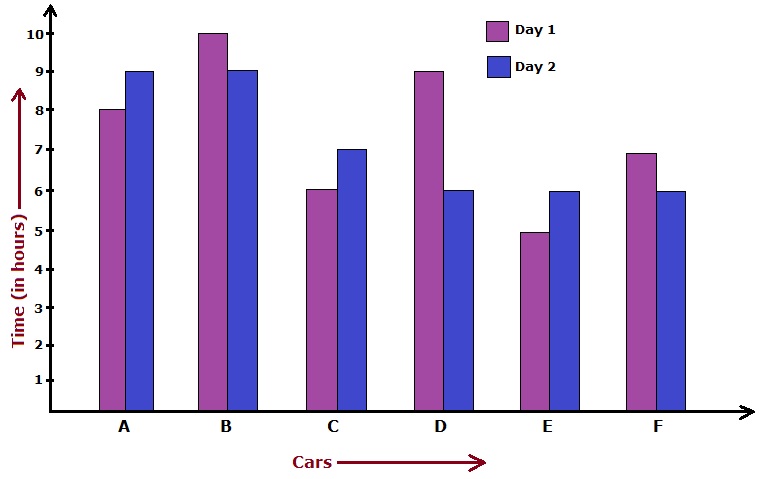
Time, taken (in hours) by six cars to cover a certain distance on two different days.
- Which one of the following cars traveled at the same speed on both days?
- A
- B
- E
- None
Answer: (d) NoneSolution: The speed of cars, on day 1. $$ A = \frac{640}{8} $$ $$ = 80 \ Km/hr $$ $$ B = \frac{830}{10} $$ $$ = 83 \ Km/hr $$ $$ C = \frac{590}{6} $$ $$ = 98.34 \ Km/hr $$ $$ D = \frac{940}{9} $$ $$ = 104.45 \ Km/hr $$ $$ E = \frac{510}{5} $$ $$ = 102 \ Km/hr $$ $$ F = \frac{825}{7} $$ $$ = 117.86 \ Km/hr $$ The speed of cars, on day 2. $$ A = \frac{780}{9} $$ $$ = 86.67 \ Km/hr $$ $$ B = \frac{725}{9} $$ $$ = 80.56 \ Km/hr $$ $$ C = \frac{630}{7} $$ $$ = 90 \ Km/hr $$ $$ D = \frac{650}{6} $$ $$ = 108.34 \ Km/hr $$ $$ E = \frac{620}{6} $$ $$ = 103.34 \ Km/hr $$ $$ F = \frac{790}{6} $$ $$ = 131.67 \ Km/hr $$ Hence none of the cars traveled at the same speed on both days.
- Find the speed of car A on day 1 in meter per second?
- 22.23 m/s
- 24.14 m/s
- 20.28 m/s
- 18.33 m/s
Answer: (a) 22.23 m/sSolution: The speed of car A on day 1 in km/hr.$$ A = \frac{640}{8} $$ $$ = 80 \ Km/hr $$ The speed of car A on day 1 in m/s.$$ = \left[80 \times \frac{5}{18}\right] \ m/s $$ $$ = 22.23 \ m/s $$
- Find the difference between the speed of car E on day 1 and the speed of car B on day 2 km/hr?
- 18.22 Km/hr
- 20.25 Km/hr
- 21.44 Km/hr
- 22.33 Km/hr
Answer: (c) 21.44 Km/hrSolution: The speed of car E, on day 1. $$ = \frac{510}{5} = 102 \ km/hr $$ The speed of car B, on day 2. $$ = \frac{725}{9} = 80.56 \ km/hr $$ Required difference $$ = 102 - 80.56 $$ $$ = 21.44 \ km/hr $$
- The distance travelled by car D on day 2 was approximately what percent of the distance travelled by car D on day 1?
- 50 %
- 69 %
- 74 %
- 77 %
Answer: (b) 69 %Solution: Required percentage $$ = \left[\frac{650}{940} \times 100\right] \ \% $$ $$ = 69.15 \ \% $$ $$ \approx 69 \ \% $$
- Find the ratio of speeds of car A on day 1 to car C on day 2?
- 3:4
- 5:6
- 7:8
- 8:9
Answer: (d) 8:9Solution: The speed of car A, on day 1. $$ = \frac{640}{8} $$ $$ = 80 \ Km/hr $$ The speed of car C, on day 2. $$ = \frac{630}{7} $$ $$ = 90 \ Km/hr $$ Required ratio $$ = \frac{80}{90} $$ $$ = 8:9 $$