Circular Permutation:
What is Circular Permutation?
The different ways to arrange the given "n" distinct objects in a circular manner is called the circular permutation. There are two types of circular permutations.
Note: In circular permutation, one element is always fixed and all other elements are arranged relative to the fixed element.
Type (1): When the clockwise and anticlockwise orders are different then:
The number of circular permutations $$ P_n = \frac{nP_r}{r} $$ Where, n = Total number of objects.
r = Number of selected objects.
\(P_n\) = Circular permutation.
If n = r (selecting all the objects) then,$$ P_n = \frac{nP_n}{n} $$ $$ = \frac{n \times (n - 1)!}{n} $$ $$ P_n = (n - 1)! $$
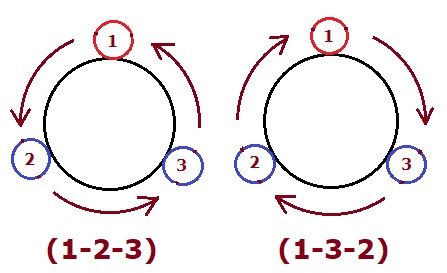
Here the arrangement (1-2-3 and 1-3-2) is different when we see the images from clockwise and anticlockwise.
Type (2):When the clockwise and anticlockwise orders are the same then:
The number of circular permutations $$ P_n = \frac{nP_r}{r} $$ Where, n = Total number of objects.
r = Number of selected objects.
\(P_n\) = Circular permutation.
If n = r (selecting all the objects) then,$$ P_n = \frac{nP_n}{2n} $$ $$ = \frac{n \times (n - 1)!}{2n} $$ $$ P_n = \frac{(n - 1)!}{2} $$
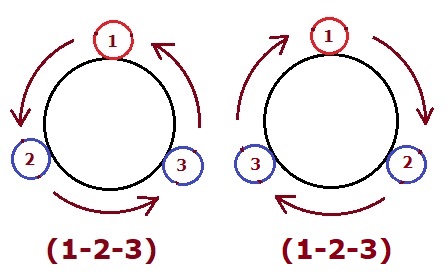
Here the image (2) is the reflection of image (1), it can not be distinguished. We can say the way of arrangement is the same (1-2-3) whether we see it from clockwise or anticlockwise.
Example(1): Find the number of ways in which three men and three women can sit around a circular table if none of any two women sit together?
Solution: Three men can sit around the circular table in \((3 - 1)!\) way = \(2!\)
Three women can sit around the circular table in the space between the men in three chairs if no two women sit together = \(3!\)
Hence required number of ways = \(2! \times 3!\) = 12 ways.
Example(2): Find the number of ways in which five different colour beads can be arranged to form a necklace?
Solution:Total number of circular permutations$$ P_n = \frac{(n - 1)!}{2} $$ $$ = \frac{(5 - 1)!}{2} $$ $$ = \frac{4!}{2} $$ $$ = 12 \ Ways $$